This episode: Lambda Functions. In this Hello, Cloud blog series, we're covering the basics of AWS cloud services for newcomers who are .NET developers. If you love C# but are new to AWS, or to this particular service, this should give you a jumpstart.

In this post we'll introduce AWS Lambda functions and write a "Hello, Cloud" in C#. We'll do this step-by-step, making no assumptions other than familiarity with C# and Visual Studio. If you've never worked with serverless, prepare to have your mind blown.

Serverless: What is it, and why use It?

Lambda functions are a form of serverless cloud computing available from Amazon Web Services. "Serverless" means you don't have to provision servers for your code to run on, apply patches, or worry about scaling. Of course there are servers somewhere running your code, but they aren't your concern. If your code needs to run, a server will spring up to run it. If your code needs to run a lot, many servers will rise to the occasion.

A Lambda function is your code configured to run in AWS in response to some trigger, such as a queue message, a new upload to S3, or a schedule timer. If you've got some C# code that needs to run in response to an event, it may be a good candidate for a Lambda function. Lambda functions can perform file processing, such as resizing images. They can perform stream processing, such as calculating analytics. They can serve the back-end code for web, mobile, or IoT applications. They can perform scheduled maintenance, such as creating a backup snapshot of a data resource. Many things you could do with a traditional farm of computing instances make sense as Lambda functions and are less work to set up.

Although serverless functions have many uses, they aren't a hammer for all nails: their execution has a time limit of 15 minutes. The ideal Lambda function is lightweight. That doesn't mean your application can't do real work, but it does mean your individual Lambda functions should be lean and mean. If you've been moving in the direction of microservices, you'll find a lot of synergy with Lambda functions.

Serverless has a refreshing payment model that is truly "pay for what you use." Cloud computing is often described as utility computing, meaning a pay-as-you-go model in which customers are charged for what they use, just like metered electrical service. What does "use" mean? It depends on the service. With many cloud services, that means you start paying by the hour/minute/second for computing resources once you allocate them, and that continues until you deallocate them—whether those resources are in constant use or not. In serverless, you only pay when your code executes. There's no worry about leaving the meter running with idle computing resources, because you don't provision any computing resources. The AWS Lambda free tier includes one million free requests per month, so get ready to do some experimenting!

Our Hello, Lambda Project

We'll use Visual Studio to create a simple "Hello, Lambda" function, deploy it to AWS, and test it. Our Lambda function will take a phone number input parameter (a string of digits) and return all the letter combinations.

With Lambda functions we have two ways of working available: we can upload a zipped deployment package, or we can upload a container. We will do a zipped deployment package here, and cover containers in a future post. At the time of this writing, the latest .NET version supported by AWS Lambda is .NET Core 3.1 for deployment projects and .NET 5 for containers. Update: Introducing the .NET 6 Runtime for AWS Lambda

source code

One-Time Setup

To experiment with Lambda and .NET, you will need:

An AWS account , and an understanding of what is included in the AWS Free Tier.
Install Microsoft Visual Studio. You can use another editor, but this blog assumes VS.
Install the AWS Toolkit for Visual Studio and configure it to access your AWS account.
Install the dotnet CLI lambda nuget packages :

dotnet new -i Amazon.Lambda.Templates
dotnet tool install -g Amazon.Lambda.Tools

Step 1: AWS Console

Let's navigate to the area of the AWS console where we'll be working.

Navigate to the AWS console and sign in.
At top-right, select the AWS Region you want to be working in from the dropdown, typically one close to your location. We're going to use N. California.
Navigate to the AWS Lambda section. You can enter "Lambda" in the search bar to find it.

Step 2: Create a New AWS Lambda Function

Now we'll create our AWS Lambda function.

In the AWS console, navigate to the Lambda > Functions page.
Click Create a Function.
Select Author from Scratch, since this will be a simple, self-contained function.
For Function name, enter hello-lambda.
Under Runtime, select the latest .NET version available. We're using .NET Core 3.1 (C#/PowerShell).
Default (but review) the rest of the settings.
Click Create Function. 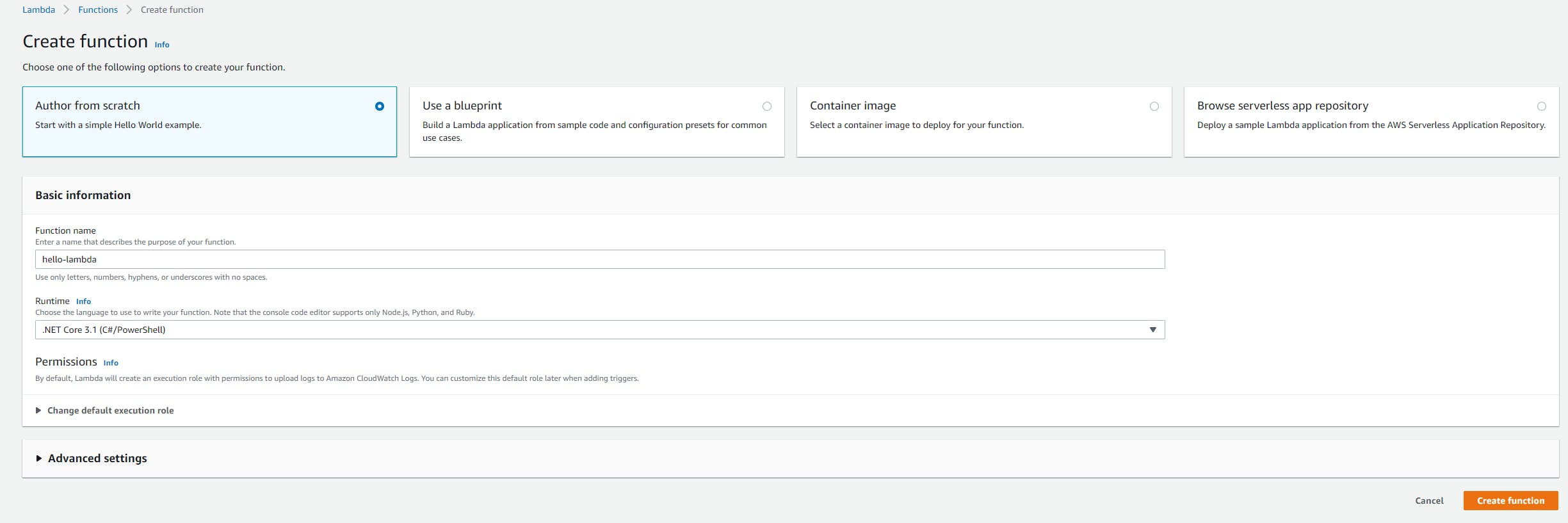The page that follows will show your configured-but-not-yet-uploaded hello-lambda function.
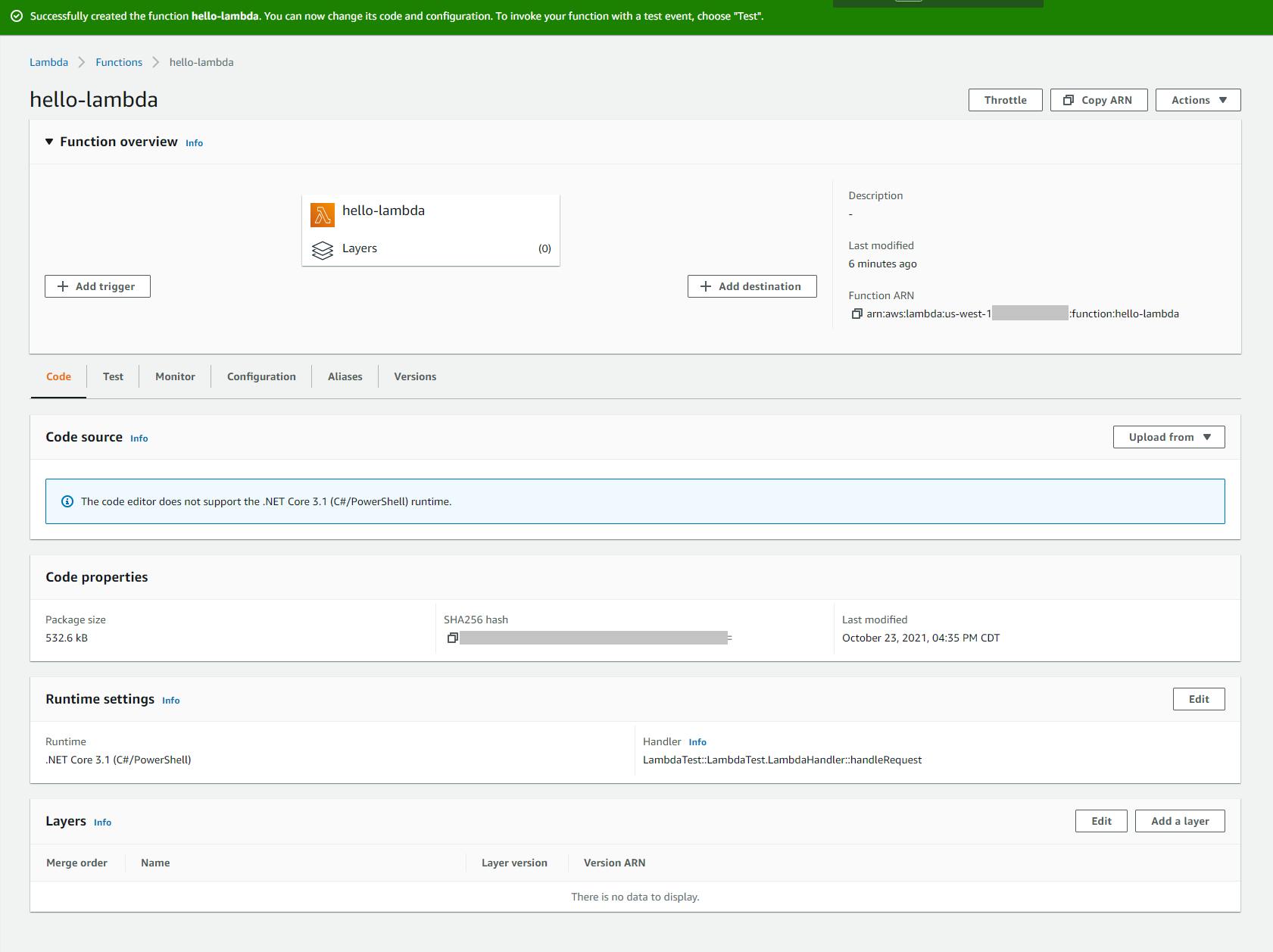
Take note of the role that was automatically generated for the function. You can find this on the Configuration tab, Permissions section. If in the future you want to deploy your function using the dotnet command, you'll need the Amazon Resource Name (ARN) for this role.

Step 3: Create a New Lambda Project with Visual Studio

Now we're ready to write our C# function in Visual Studio.

Launch Visual Studio and select Create New Project.
Browse/search/filter for AWS Lambda Project (.NET Core - C#) and select it. Then click Next.
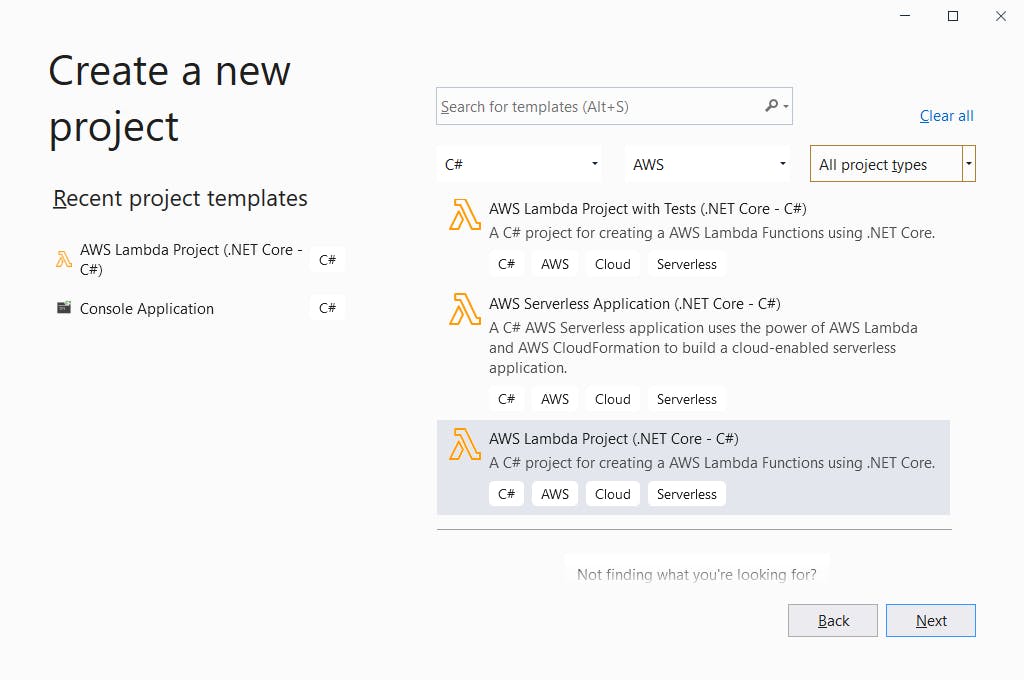
On the next page, enter the Project name hello-lambda.
Enter your preferred folder location.
Click Create.
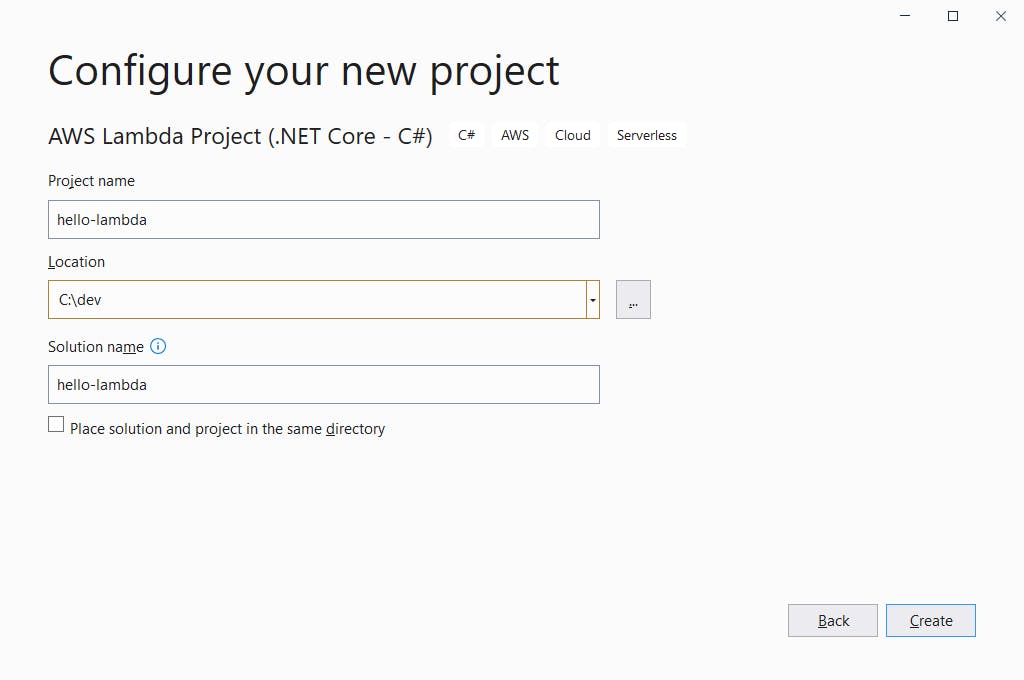
On the next page, select the Empty Function blueprint.
Click Finish. 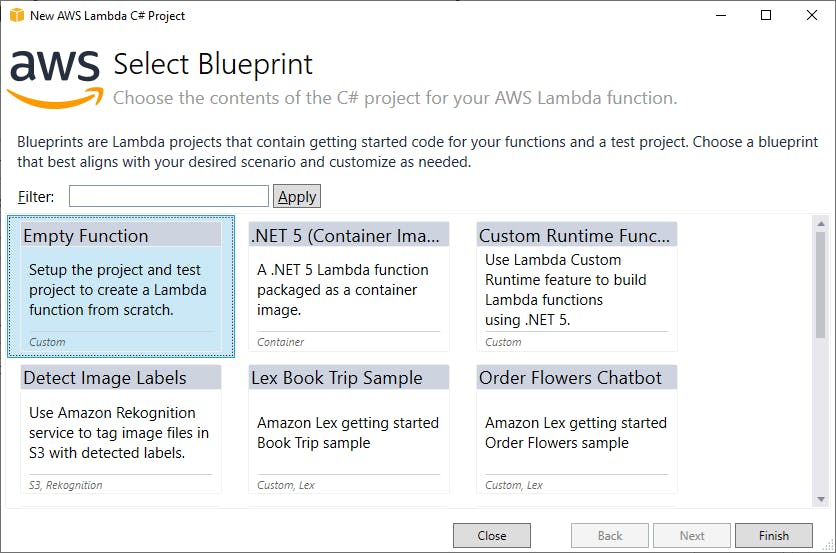Moments later, your project has been created.

Take note that this step could alternatively have been accomplished in a command window or terminal window, with the dotnet new command.

Step 4: Code Your Lambda Function

Now we'll replace the generated Lambda function with our own.

In Visual Studio Solution Explorer, double-click the readme file and read about what has been created: a simple function that takes an input string and returns an upper-case version of it. The readme also has instructions on deployment and testing.
Double click the Function.cs file to edit it. Note how simple the provided function is.
Replace the code in Function.cs with the version below.
Build your project.

I cannot take any credit for this wonderfully succinct LINQ code, which I found on StackOverflow and couldn't identify the author. It's a good reminder of how powerful C# is!

using System;
using System.Collections.Generic;
using System.Linq;
using System.Threading.Tasks;

using Amazon.Lambda.Core;

// Assembly attribute to enable the Lambda function's JSON input to be converted into a .NET class.
[assembly: LambdaSerializer(typeof(Amazon.Lambda.Serialization.SystemTextJson.DefaultLambdaJsonSerializer))]

namespace helloLambda
{
    public class Function
    {
        /// <summary>
        /// Returns the letter combinations for a phone number.
        /// </summary>
        /// <param name="input">digits-only string</param>
        /// <param name="context">ILambdaContext</param>
        /// <returns>string array of letter combinations</returns>
        public IEnumerable<string> FunctionHandler(string digits, ILambdaContext context)
        {
            if (string.IsNullOrEmpty(digits) || digits.Any(c => c < '0' || c > '9')) { return new List<string>(); }
            string[] phone = new string[] { "0", "1", "ABC", "DEF", "GHI", "JKL", "MNO", "PQRS", "TUV", "WXYZ" };
            return digits.Skip(1).Select(d => d - '0').Aggregate(phone[digits[0] - '0'].Select(c => c.ToString()), (acc, i) => phone[i].SelectMany(c => acc.Select(a => $"{a}{c}")));
        }
    }
}

Step 5: Deploy Lambda Function to AWS

Now we'll deploy our function to AWS. We can do that right from Visual Studio, thanks to the AWS Toolkit. Take note, however, that there are 3 different ways you can publish your function to AWS:

A. With Visual Studio.

B. Using the dotnet command. If you use this method, you'll need to specify the ARN of the role that AWS generated for you in Step 2.

dotnet lambda deploy-function hello-lambda --function-role <role>

C. From the AWS console, via the Upload from button.

Today we'll use Visual Studio to publish.

In Solution Explorer, right-click the hello-lambda project and select Publish to AWS Lambda.
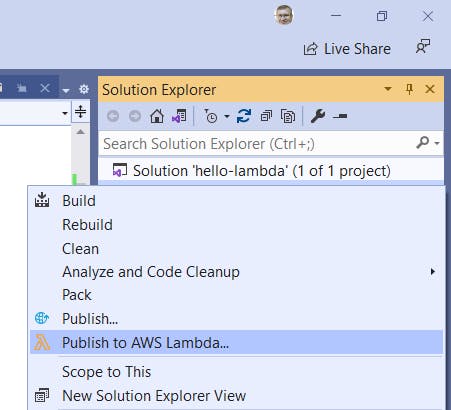
In the Upload Lambda Function dialog, select the target Lambda function (hello-lambda) and enter a description.
Set Handler to hello-lambda::helloLambda.Function::FunctionHandler. This value must be of the form assembly::class::method and exactly match the assembly, class, and method names of your function, or invocation will fail. In our case, the assembly name is hello-world, the class name (including namespace) is helloLambda.Function, and the method name is FunctionHandler.
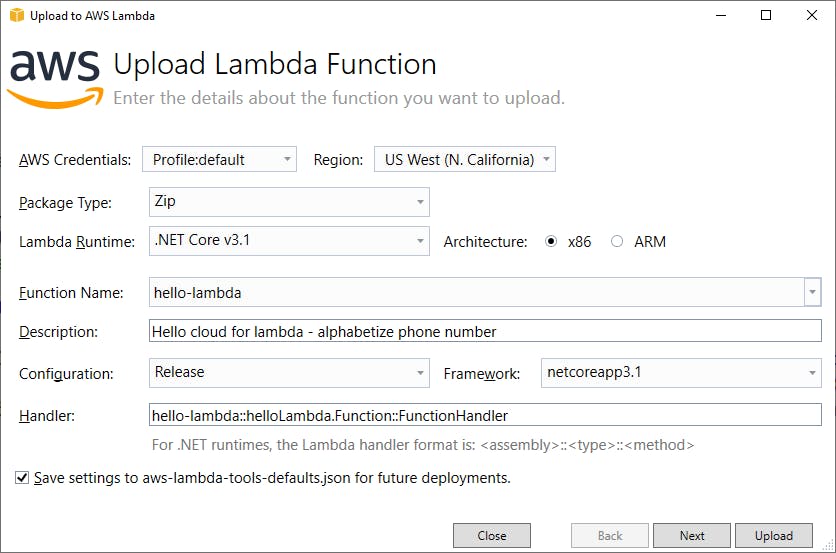
Click Upload and wait for the function to upload. If the Next and Upload buttons are disabled, check that you filled out everything on the dialog, and that the Handler value is correct.

Publishing with the Dotnet Command

Deploying from Visual Studio is great, but you'll eventually want to use a CI/CD pipeline to deploy your functions. We could have published to AWS using the dotnet command. If you use this method, you'll need to specify the ARN of the role that AWS generated for you in Step 2. Open a command/terminal window, CD to your project location, and enter

dotnet lambda deploy-function hello-cloud --function-role <role>

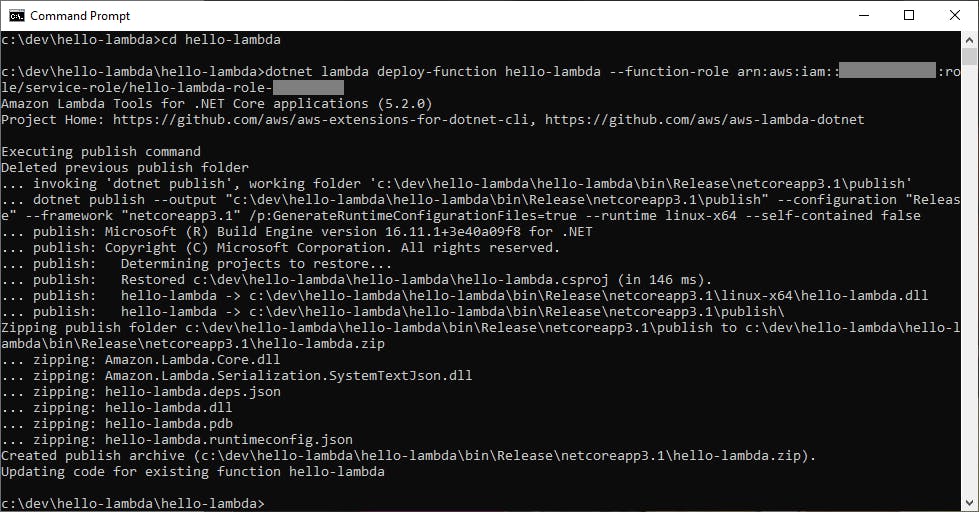Voila, our function is deployed!

Step 6: Test the Lambda Function

With our AWS Lambda function deployed, we can test it. Well do that from Visual Studio in this post, but be aware that there are 3 ways you can test your function:

A. In Visual Studio, using the Lambda function test tool.

B. Using the dotnet command:

dotnet lambda invoke-function hello-lambda --cli-binary-format raw-in-base64-out --payload "2345678"

C. Using the AWS Console. When viewing your Lambda function, there is a Test tab where you can create test payloads and run tests.

We're using Visual Studio today.

Since we deployed with Visual Studio in Step 5, you should already be on the Lambda test page in Visual Studio.
In the Sample Input large text box, enter "234567", or any phone number you wish to test.
Click the Invoke button.
Your function executes, and the output is shown at right in the Response area. We see many alphabetized phone numbers. Hold the phone, it worked!
Note the RequestID and duration in MS for the function execution.
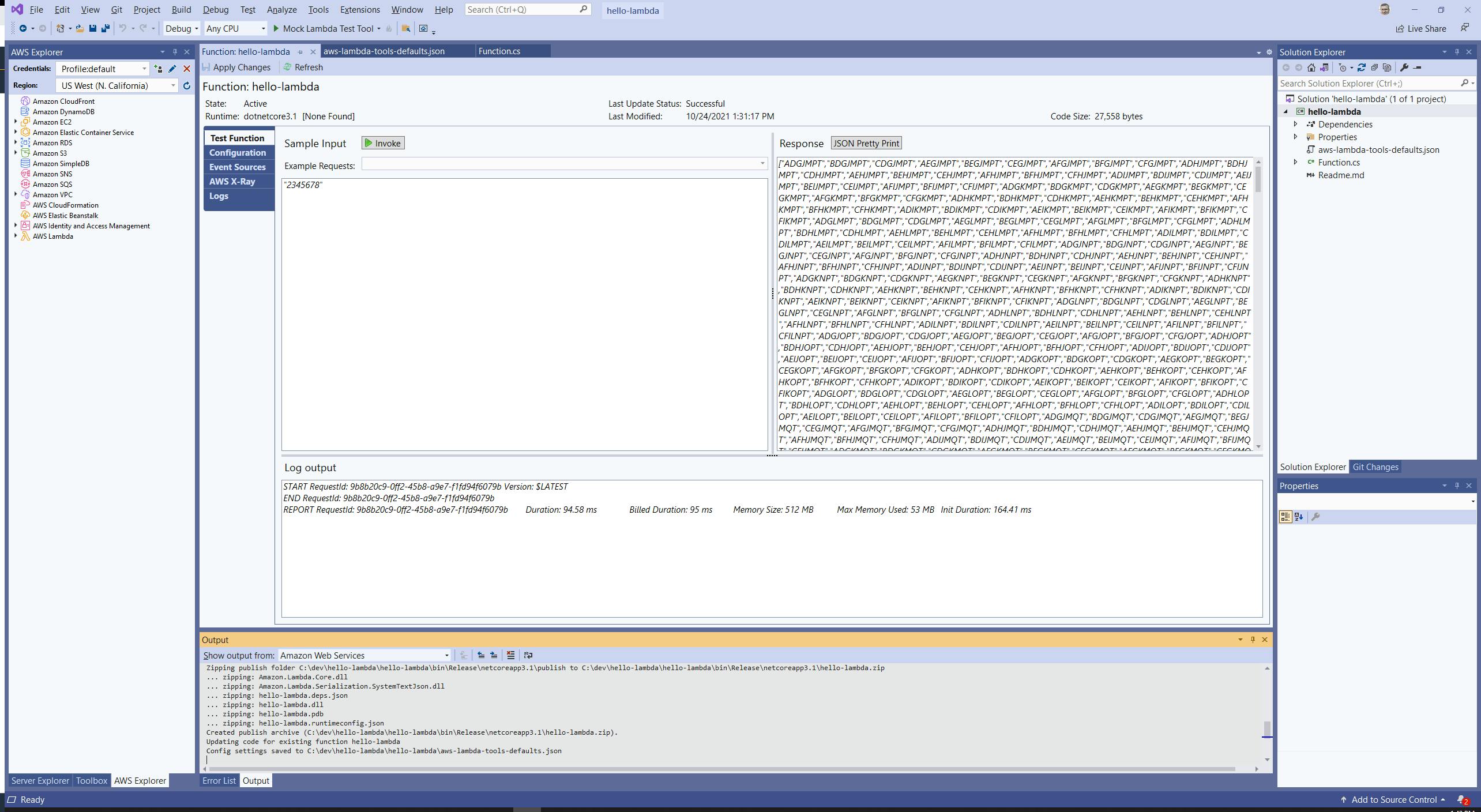
Try out some different values, including valid (digits-only) and invalid input.

Testing with the Dotnet Command

Let's contrast what we just did with testing with the dotnet command. Open a command/terminal window, CD to your project location, and enter

dotnet lambda invoke-function hello-lambda --cli-binary-format raw-in-base64-out --payload "1234567"

Our function is invoked, and we see the response. Very cool. 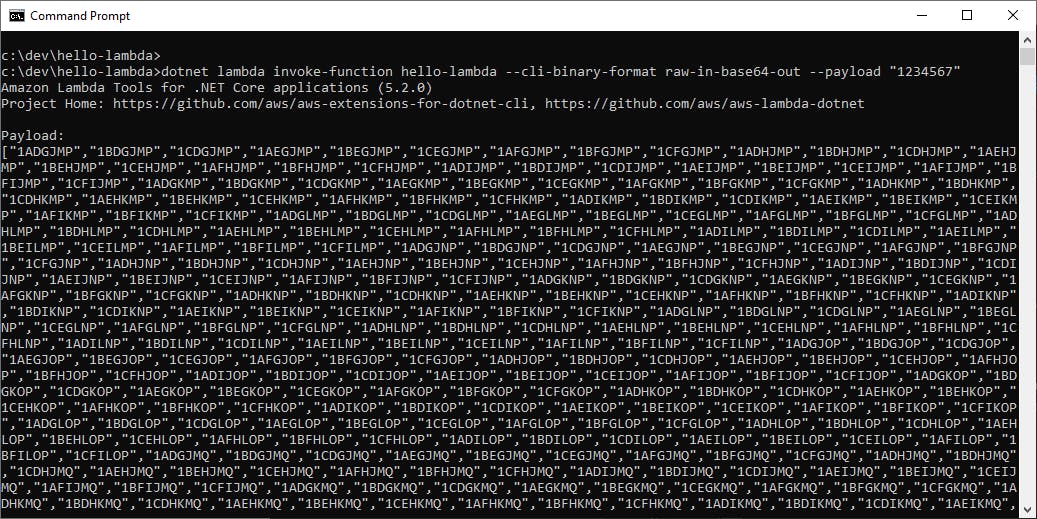On your own: practice testing your function in the AWS console.

Step 7: Review Logs in the AWS Console

We've been doing so much from Visual Studio, how can we be sure what we just did really ran in the cloud? Using the AWS console, we can review logs for our service execution.

In the AWS Console, navigate to Lambda > Functions and view the hello-lambda service.
Select the Monitor tab. You'll see recent invocations. The topmost (most recent) invocation's RequestID and DurationInMS values should match what was displayed in the Visual Studio Lambda function test tool.
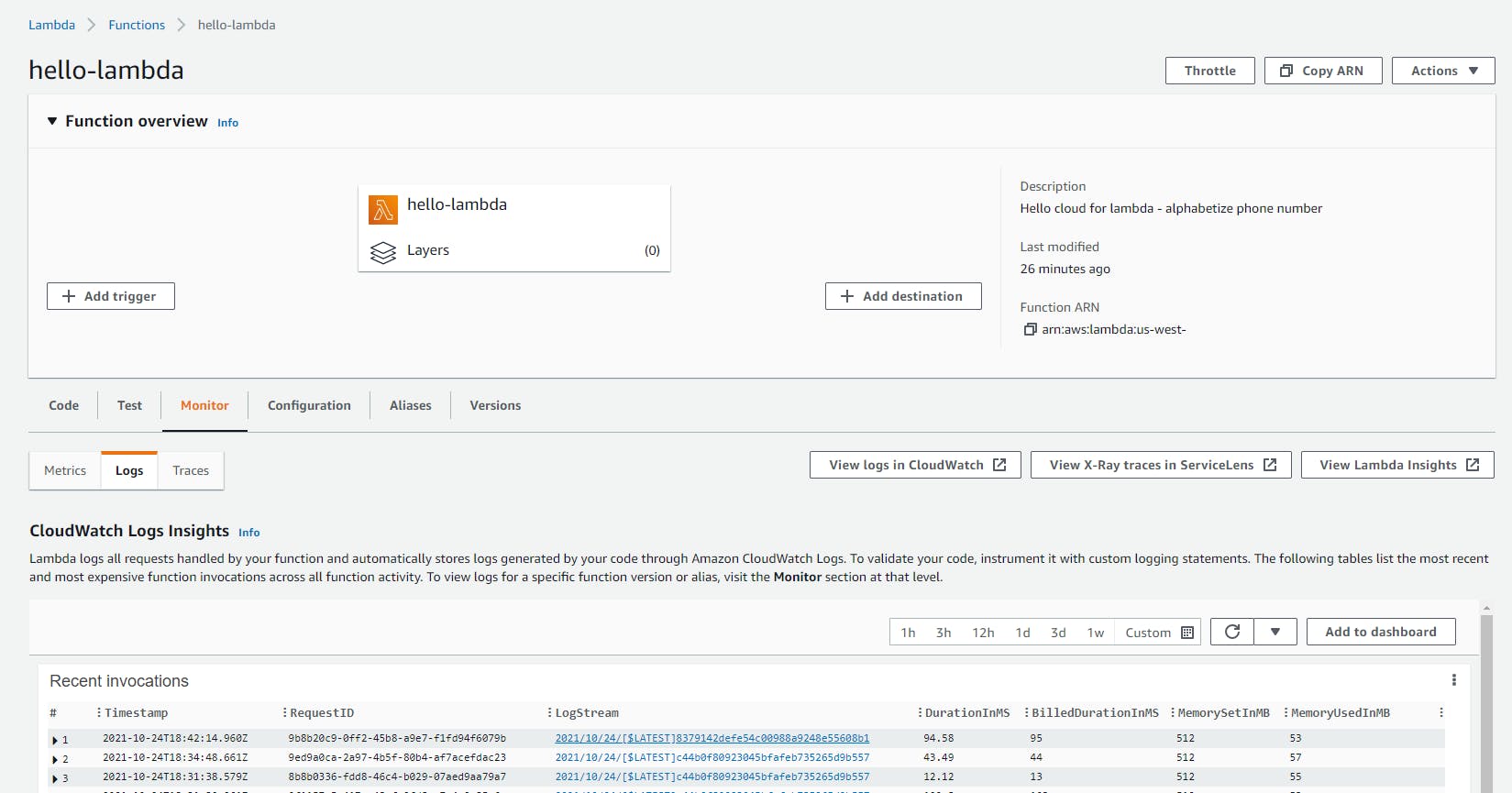
Click the LogStream link for the invocation. Now you're looking at the execution log for the function. Although there's not much here other than starting and completing the run, this is where you would go to debug issues with real functions, including details about calls to other AWS services and exceptions.

Tip: your function code can write messages to the execution log, using

context.Logger.LogLine(<message>);

Step 8: Delete the Function

When you're done with hello-lambda, remember to delete it. As a general rule, I advocate having an exit strategy for anything you create in the cloud. It's a good habit to get into, and helps avoid unexpected charges.

Navigate to Lambda > Functions.
Check the check box next to hello-lambda.
From the Actions menu, select Delete and confirm.

Congratulations! You're on your way to serverless greatness with .NET and AWS.

Where to Go From Here

In this post we've gotten a first taste of AWS Lambda and the power and simplicity of serverless. In an actual Lambda function for an application, you would also configure an event to trigger the function. You do that in the AWS console, Configuration tab, Triggers section. Beyond the event trigger, your function might also need to interact with other AWS services such as SQS or DynamoDB and/or route its response somewhere. You might front your Lambda back-end functions with AWS API Gateway.

If this was your first taste of serverless, your head should be filled with ideas and questions. Go and build something real, it's the best way to learn. If you're worried you don't have enough control over the runtime environment, rest assured you can configure how much memory your functions get or what processors they run on, which affects your cost. Your functions can even run on ARM processors.

You have many choices in .NET AWS Lambda functions. You can use deployment packages like we did here, or use containers. You can use Visual Studio, the dotnet command, or the AWS console to deploy and test your functions. In this post we used Visual Studio to create our Lambda function, publish it to AWS, and test it. It's a good idea to experiment with the different options.

Some other "Hello, World" on Lambda blog posts are linked below, to give you a variety of perspectives and ways of working. My colleague Bryan Hogan has a blog series that progresses from a Hello World Lambda all the way to a .NET Web API powered by Lambda that uses containers.

Hello, Lambda

Getting Started with .NET on AWS: Lambda Functions

Table of contents